Coral X-radiograph Densitometry System

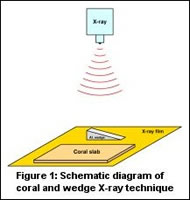When two materials (e.g., coral sample and aluminum standard) are X-rayed (Figure 1) and the exposed film exhibits equal optic density for both materials, the density of the sample material can be calculated (Buddemeier, 1974; Chalker et al., 1985) from:

(t_m)_s · rho_s · eta_s = (t_m)_st · rho_st · eta_st (1)

(t_m)_st = mass absorption coefficient of standard

(t_m)_s = mass absorption coefficient of sample

rho_st = density of standard

rho_s = density of sample

eta_st = thickness of standard

eta_s = thickness of sample

Solving for density of the sample:

rho_s = ((t_m)_st / (t_m)_s) · (eta_st / eta_s) · rho_st (2)

Hence, one can find density of the specimen from film transparency if one knows:

1. the thickness of the standard (eta_st) and the thickness of the sample (eta_s).
2. the density of the standard (rho_st).
3. the mass absorption coefficient ratio of standard to sample ((t_m)_st / (t_m)_s)

Buddemeier (1974) obtained the mass absorption coefficients from tabulated values, but the method required the exact determination of the energy of the X-ray beam (continuous converted to single), voltage of machine, and composition of material. Chalker et al. (1985) avoided such problems by using relative mass absorption coefficients. They determined the relative mass absorption coefficient of the standard and sample by slopes of curves fitted to data of sample thickness versus densitometer output voltage.

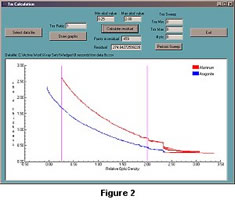
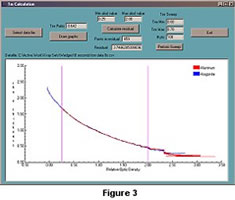
CoralXDS employs a modification of the Buddemeier and the Chalker et al. methods. Digitized X-radiographs and computerized image processing are used instead of densitometer voltages. Instead of a step wedge or tubes of material, triangular wedges of known dimensions and density (aluminum and aragonite) are used to obtain a relationship between optic density and thickness. Absolute values for the mass absorption coefficients are not needed because the relative mass absorption coefficient ratio is determined by curve fitting. Since ((t_m)_st / (t_m)_s) is a constant ratio the term t_mr can be substituted:

rho_s = t_mr · rho_st · (eta_st / eta_s) (3)

The t_mr for the aluminum (Al) and aragonite (Ar) wedges is determined by plotting relative optic density versus rho · eta. The value of t_mr that minimizes the sum of the residuals |tmr Al - Ar| is determined. Figure 2 shows the offset for the unadjusted aluminum and aragonite data. Figure 3 shows the data fit with a t_mr of 0.642.

Coral samples are commonly collected by coring. A core is medially sectioned producing slabs approximately 5 to 10 mm thick. The slab is planed with a precision surface grinder to ensure the slab is parallel sided of uniform thickness (Figure 4).

The coral slab and the aluminum wedge are placed on a sheet of 8" x 10" X-ray film. The film is placed on a lead vinyl sheet and aluminum plate. The film is X-rayed at 50 KvP and 10 mA with a source to object distance of 1.25 m for 5 to 15 seconds based on slab thickness and density. Another film is then placed in the same position and covered with an aluminum sheet of thickness equal to the coral slab and X-rayed at the same settings for use as a background image. The resulting X-radiographs of the coral sample and the background are digitized using a medical X-ray scanner (Figure 5). At the same setting, a transparent ruler is digitized in a vertical and horizontal position for use in the scale calibration.

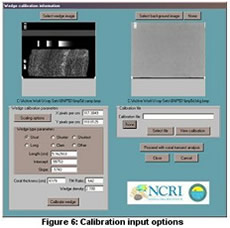CoralXDS is a Windows-based program used for densitometric analyses on X-radiographs of coral slabs. The required inputs are dimensions and density of the aluminum wedge, thickness of the coral slab, the relative mass absorption coefficient ratio, and images of the coral X-radiograph, background X-radiograph, and scale bar/ruler (Figure 6).

CoralXDS can also be used in extension/luminance mode, which is a less complicated application than the full extension, density, and calcification mode. This mode allows the rapid calculation of linear extension for annual and sub-annual coral growth bands. The required inputs for the use of CoralXDS in extension/luminance mode are an image of the coral X-radiograph, and knowledge of the scaling parameter (pixels per centimeter) used for the image.

To determine the relationship between relative optic density (ROD) and skeletal density rho_s, a transect is selected along the wedge. Transect pixel luminances are converted to optic density using:

ROD = log₁₀(background luminance / sample luminance) (4)

ROD values are averaged perpendicular to the wedge transect axis to give ROD as a function of distance along the wedge, or equivalently, as a function of wedge thickness. Using equation (3), rho_s is determined as a function of wedge thickness eta_st since t_mr , eta_s , and eta_st are constant. This provides data pairs of ROD and rho_s. Two 4th order curves are fit through the data pairs (Figure 7) yielding continuous calibration curves of ROD vs. rho_s.

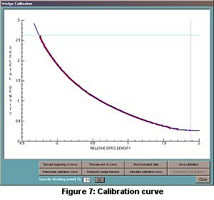
A rectangular transect is selected on the coral image. Using the previously derived calibration curve, the pixels within the transect are converted into skeletal density values and then averaged over the width of the transect. Skeletal density is plotted as a function of distance along the coral transect as shown in Figure 8.

Using transect density data, high-density (HD) and low-density (LD) bands are determined by three methods: Half Range (HR), 2nd Derivative Zero (2DZ), and 2nd Derivative Maximum (2DM). Once HD and LD band portions are delimited, extension can be defined and calcification calculated. Annual bands are defined by a pair of adjacent HD/LD bands and also by peak to peak and valley to valley density (PV) values. Figure 9 shows examples of the delimiting methods.

The HR method delimits bands based on the mean of adjacent density maxima and minima. The 2DZ method delimits bands by the inflection point between density maxima and minima. The 2DM method delimits bands based on 2nd derivative maxima bounding a density maximum.

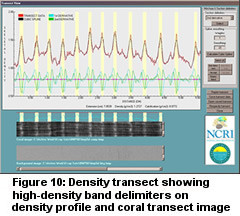
Figure 10 illustrates the 2DZ delimiting method. A cubic spline curve is calculated for the skeletal density data. The 1st and 2nd derivatives are calculated. Zero crossings of the 2nd derivative associated with a density maximum are used to delimit the HD and LD bands. This provides an objective means of band determination.

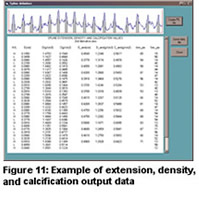
Figures 11 and 12 show examples of the output data for extension, density, and calcification for high-density, low-density, and annual bands.

Radiographic image quality is subject to variations in beam intensity including backscatter, edge-effects/magnification, the inverse square law, and the anode heel effect (Carlton and Adler, 1996). Backscatter is minimized by placing the film on a 1 mm equivalent lead vinyl sheet. Edge-effects depend on the source to object distance (SOD), source to image receptor distance (SID), and location relative to the central ray. Edge-effects at the furthest point from the central ray (6.4cm) on a typical 8" x 10" film for a 0.5-cm-thick object is 0.026 cm. Image magnification under the central ray at a SID of 125 cm is about 0.4%. Neither backscatter nor edge-effects/magnification impart a significant effect for the described system.

The inverse square law states that intensity at a given distance from a point source is inversely proportional to the square of the distance. Thus intensity decreases by this relationship moving away from the central ray.

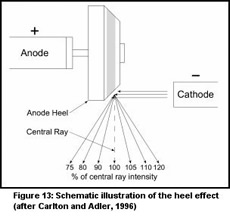The heel effect is produced by the geometry of an angled anode target where photons hitting the target toward the anode end (the heel) tend to be more absorbed by the target (Figure 13). This can result in significant variation in beam intensity along the anode-cathode axis. The use of an X-ray background image minimizes the impact of the inverse square law and the heel effect on the derived skeletal density of the coral.

Errors associated with program methodology are sample thickness and wedge calibration.

To investigate the errors in skeletal density calculation due to variations in sample thickness, let:

rho_s' = calculated sample density

eps = sample thickness error

deltarho = error in density calculation

Using equation (3),

rho_s' = t_mr · rho_st · eta_st/(eta_s + eps) (5)

deltarho = |rho_s - rho_s'| = t_mr · rho_st · eta_st · eps/(eta_s · (eta_s + eps)) (6)

For a 0.5 cm slab with a thickness error of 0.001 cm (tolerance of the surface grinder), the density error is 0.004 g/cm3 or about 0.2%.

By incorrectly specifying the thick edge of the wedge during calibration, an error in actual standard thickness eta_st at all points along the wedge is induced, thereby producing an error in sample density rho_s. To determine the magnitude of this error in sample density, let:

t_mr = relative mass absorption coefficient ratio

rho_st = density of standard

rho_s = density of sample

rho_s' = calculated sample density

eta_s = thickness of the sample

H = height of the wedge at the thick edge

L = length of wedge

eps = error in the specification of the wedge edge

eta_st(x)= thickness of wedge at a distance x from the thick edge of the wedge

eta_st(x) is given by

eta_st(x) = H · (1 - x/L) (7)

Equation (7) illustrates the linear relationship between thickness of the wedge and distance along the wedge.

When the edge of the wedge is incorrectly specified by a distance eps, the actual and measured sample densities (at an arbitrary position x₀) are given by:

rho_s = t_mr · rho_st · eta_st(x₀)/eta_s

rho_s' = t_mr · rho_st · eta_st(x₀')/ eta_s (8)

where x₀' = x₀ + eps

The density error associated with an error in the determination of the wedge edge during calibration is given by:

deltarho = |rho_s - rho_s'| = t_mr · rho_st/eta_s · |eta_st(x₀) - eta_st(x₀')| = t_mr · rho_st/eta_s · (H · eps)/L (9)

For a single pixel offset in calibration, the density error is 0.006 g/cm3 or about 0.3%.